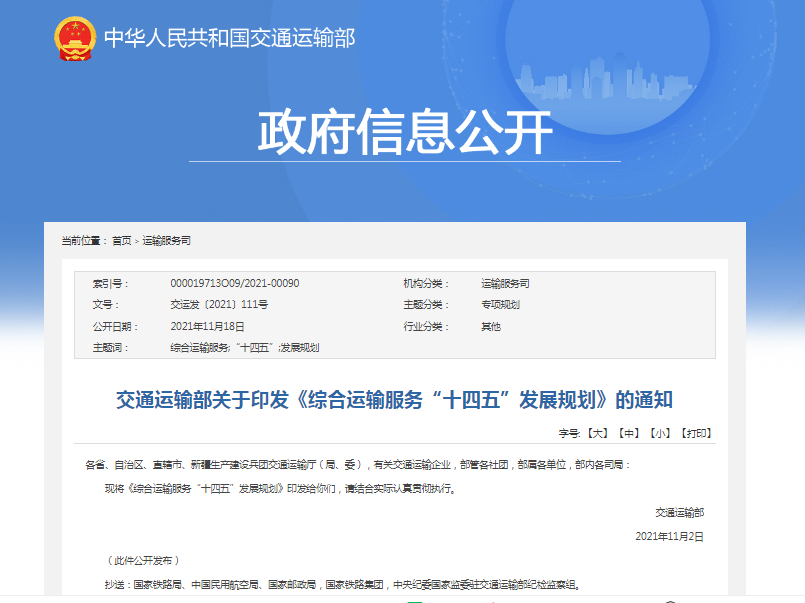
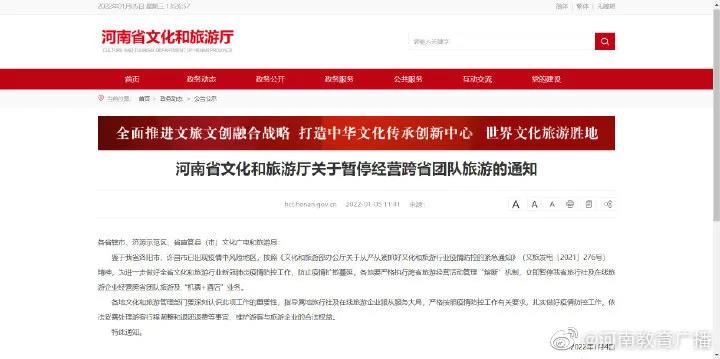
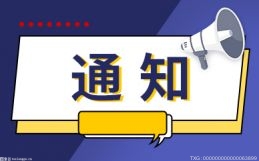
“用我的方法,‘黎曼猜想’已经被证明了”,9月24日,89岁的迈克尔·阿蒂亚在2018海德堡获奖者论坛上展示了他对“黎曼猜想”难题的证明结果。
结果有待商榷
迈克尔·阿蒂亚用“简单”的5页纸叙述了他的研究内容。
他在摘要中写道:通过理解量子力学中的无量纲常数——精细结构常数,并将此过程中发展出来的数学方法用于解决黎曼猜想。
物理学科普作家、科学网博主张轩中从物理的角度向《中国科学报》记者做了分析,他表示,精细结构常数是一个会“跑动”的数,描述两个电子相互吸引力大小,它的耦合常数随着时间的变化而变化,并不是一个“真的常数”。
“但阿蒂亚直接论证了精细结构常数是固定的,大约等于1/137,这让物理学家很费解,对第一步就产生了怀疑。”张轩中说。“也许在数学上是对的,毕竟阿蒂亚也是懂物理的,可能他有独到的见解,但这个还需要时间论证。”
中国科学院数学与系统科学研究院研究员贾朝华也对《中国科学报》记者说,“立刻对阿蒂亚的研究做分析解读,会是一件很困难的事情,这需要专家们经过较长一段时间的研究探讨。”
令数学家如痴如醉的“猜想”
“简单来说,‘黎曼猜想’是关于素数(又叫质数)的问题,是为了研究素数分布规律。”贾朝华说。
在小学五年级,我们的数学课本中第一次出现了“素数”的概念:一个大于1的自然数,除了1和它自身外,不能整除其他自然数的数叫做素数。这样一个简单却粗略地描述,使得数学家们为寻找一个更为精确地表达公式而“前赴后继”。
每个自然数都可以表示成素数因子的乘积,素数构成了正整数的基本元素。也就是说,素数的地位相当于生命世界里的DNA。
“这是数论最基本的内容,相当于一座大厦的地基,这就是它最大的‘用处’和意义。”贾朝华说。只有认识素数的分布规律,才能对数论有更深入地理解。
在黎曼之前,欧几里得用初等方法证明了素数有无穷多个;欧拉用数学分析方法引入了表达公式,描述素数的分布情况;数学大师高斯和勒让德通过大量数值计算,提出了“不大于N的素数分布密度接近N的对数函数的倒数”的猜想,后被证明,成为“素数定理”。
但是,数学家们对于“精确和清晰”的追求从未停歇。1859年,德国数学家黎曼发表了一篇题为《论不超过一个给定值的素数的个数》的文章,这是他在解析数论领域发表的唯一一篇文章,文字简练,仅仅8页纸,却成为该领域内最经典的文章。
黎曼认为,素数的分布奥秘与一个复杂的函数密切相关,而使这个函数取值为零,即非平凡零点对素数分布的精确规律有着关键性影响,他在文中定义了一个被后世成为“Zeta”的无穷极函数,这也是他开辟的一条独特路径:从一维直线拓展到复数平面中研究素数分布。
黎曼猜测,可能所有非平凡零点都全部位于实部等于1/2的直线上,这条线被称为临界线。这就是令后世数学家魂牵梦绕却辗转反侧的“黎曼猜想”。
一个半世纪以来,进展甚微。但黎曼指引了新方向,比如,37年后,法国数学家哈达玛和比利时数学家普森独立证明了素数定理,它描述了素数的大部分分布规律。
“大师指路,后继者实现。”贾朝华说。
“黎曼猜想”偶遇物理学
“黎曼猜想”有什么用?一代代数学家为之孜孜不倦究竟为了什么?
对于数学家们来说,这是探索未知,用简洁地数字和公式语言描绘复杂世界,让事物变得更清晰的过程,“这是很奇妙的。”
事实上,纯粹数学的美也在于此。在贾朝华看来,“黎曼猜想”最大的意义,首先在于大胆的猜测,另外指出了复数函数零点与素数个数如何联系。“非得说实际用处,反而贬低了‘黎曼猜想’的重要性和地位。”
后来,人们利用素数的规律之谜,发明了RSA公钥加密算法,作为难以破译的密码,素数找到了“用武之地”。
伴随着零点在临界线上分布规律的研究突破,人们发现黎曼猜想与复杂的物理现象竟然有神秘的关联。
1972年,数学家蒙哥马利与物理学家戴森在普林斯顿高等研究院偶遇,碰撞出了神奇火花——“如果将黎曼临界直线上的零点和实验记录的大原子的核的能级相比较,两者的分布惊人的相似。”这让纯粹数学触及真实空间,在量子体系等经典的混沌系统中熠熠生辉。
在纯数学领域探索百余年而无路可寻,人们转而向其他领域寻找办法。
正如迈克尔·阿蒂亚的研究,他报告后,有数学家坚定支持,“阿蒂亚先生已经到了无可挑剔的年龄。”
尽管质疑态度还是居多,尽管一时难以给出判断,但迈克尔·阿蒂亚站在物理学的角度,也许为黎曼猜想的解决指出了新方向。
-
浙江杭州夫妻醉酒老公床上酣睡妻子倒挂窗外 提醒:理性饮酒安全第一
头条 22-01-21
-
美国爸爸辅导孩子写汉字气到崩溃一行字写了3小时!网友:这跟国籍无关
头条 22-01-20
-
绝望! 女子隔离14天通过监控看狗子把家拆完 网友:感到“崩溃”
头条 22-01-20
-
辽宁沈阳男子冬天醉卧路边冻掉4根手指!网友:多亏被人发现
头条 22-01-18
-
重庆一孕妇剪毁婚庆店内32件婚纱礼服当事人发文
头条 22-01-17
-
中国空间站与国际空间站一张对比图火了 网友直呼:画面引起舒适
头条 22-01-13
-
辟谣!800多人被拉定边沙漠去隔离?西安网警:假的!
头条 22-01-11
-
生日蛋糕上插满课本男孩崩溃大哭 妈妈:想提醒他好好复习
头条 22-01-11
-
男子地铁摸女性屁股被扇3分钟耳光?警方通报
头条 22-01-06
-
天津高速现驼鸟奔跑 官方回应:系车主运输途中不慎掉落已被车主领回
头条 22-01-05
-
长得挺特别!菠萝味草莓一斤150元 网友:直接买个菠萝吃不好吗
头条 22-01-05
-
“秦始皇”做核酸珍贵画面流出?逗乐网友!调侃:“秦始皇也要核酸了!”
头条 21-12-31
-
985大学硕士妈妈吐槽儿子是学渣:他爸气得2次心梗!以后只希望孩子健康成长
头条 21-12-31
-
查干湖“头鱼”拍出299.9999万的天价!网友:怎么吃才体现它的身价
头条 21-12-29
-
村主任用洒水车向摊位喷水?官方回应:责令其辞去村委会主任职务
头条 21-12-27
-
“外教辱骂防疫人员”,西安警方回应:已成立工作专班进行调查
头条 21-12-27
-
破防了!91岁奶奶和8岁猫咪的对话让人泪崩 网友:祝愿老人健康长寿
头条 21-12-23
-
5岁女童配合消防员教科书式自救 网友点赞:很勇敢!
头条 21-12-23
-
大爷被困电梯淡定唠嗑等救援 网友:为大爷的冷静沉着点赞!
头条 21-12-22
-
男子4万元存款18年后却被银行告知存款已被支取仅剩10块钱 法院:银行赔!
头条 21-12-20
-
深圳一男子加油站拔油枪点燃后逃跑 警方已介入调查纵火人员已锁定
头条 21-12-17
-
这位感动千万抖音网友的河南“留虾女孩” 入选央视年度短片《2021看见笑容》
头条 21-12-17
-
泪目!95岁妈妈病床前亲吻74岁生病的女儿 网友:孩子不管多大都是妈妈的宝贝
头条 21-12-15
-
川妹子抽中50颗榴莲直呼吃不完!网友:可以共享你的负担吗?
头条 21-12-15
-
河南省政府发布2022年元旦放假通知
头条 21-12-15
-
濮阳市聚碳新材料产业联盟成立
头条 21-12-15
-
周口机场预计什么时候建好?都有到哪些城市的航线?官方回复来了
头条 21-12-15
-
预计明年超50家企业回归,瑞银称中概股H股上市将继续升温
头条 21-12-15
-
新乡发现一境外输入奥密克戎病例密接者,活动轨迹公布
头条 21-12-15
-
河南:中药配方颗粒不得在医疗机构以外销售
头条 21-12-15
-
中原环保完成发行5亿元超短融,利率2.95%
头条 21-12-15
-
南阳市政府将与中车四方所在新能源装备等领域开展深入合作
头条 21-12-15
-
郑州出台新措施:公租房可“掌上”缴租秒办理
头条 21-12-15
-
国家统计局:11月社会消费品零售总额增长3.9%
头条 21-12-15
-
中国11月规上工业增加值同比增长3.8%
头条 21-12-15
-
1207万!全年就业超额完成预期目标
头条 21-12-15
-
河南凯旺科技公开发行2396万股新股,获6321.47倍申购
头条 21-12-15
-
事关货币政策、房地产、全面注册制,一行两会划定明年工作重点
头条 21-12-15
-
隔夜欧美·12月15日
头条 21-12-15
-
多部委密集部署明年工作!三大看点值得关注
头条 21-12-15
-
立方风控鸟·早报(12月15日)
头条 21-12-15
-
医药巨头今日登陆科创板!高瓴重仓"陪伴",引入"绿鞋"机制
头条 21-12-15
-
皮海洲:临门一脚踏刹车!龙竹科技终止转板说明了什么
头条 21-12-15
-
立方风控鸟·晚报(12月14日)
头条 21-12-14
-
成渝地区双城经济圈建设2022年拟推进160个重大项目,投资约2万亿元
头条 21-12-14
-
总投资额超百亿!中建七局接连中标两个EPC总承包项目
头条 21-12-14
-
2022年部分地方债提前下达,财政提前发力稳经济
头条 21-12-14
-
信阳华信投资集团10亿元中票完成发行,利率3.70%
头条 21-12-14
-
新强联拟择机出售所持明阳智能股票
头条 21-12-14
-
洛阳新强联拟亿元入股山东拟IPO公司,持股4.50%
头条 21-12-14
-
焦作在这场推介会上现场签约28个项目,总投资240亿元
头条 21-12-14
-
河南7种轻微交通违法可免罚
头条 21-12-14
-
广州高校发现古墓考古专业出动!网友:这不巧了嘛!毕业论文自己找来了
头条 21-12-14
-
浙江乐清民警自曝37岁未婚救下轻生女子 网友:一定要最爱自己
头条 21-12-14
-
画面感太强!主人出差猫咪打开水龙头把家淹了 网友:当然是原谅它
头条 21-12-09
- 加盟大平台,继往又开来!怡亚通全球招募合2022-01-25
- 伊利新春迷你剧《我耀我家》:关于春节和冬2022-01-25
- 360金融课堂学员:误入杀猪盘后的重生与成长2022-01-25
- 2021年全国海关查扣进出口侵权嫌疑货物7.92022-01-25
- 相约冰雪,一起来丨逐梦前行2022-01-25
- 国家卫健委:昨日新增确诊病例45例 其中本2022-01-25
- 相约冰雪,一起来|以中国速度完成冰雪运动2022-01-25
- 超全科普!一次看懂北京冬奥15个比赛项目2022-01-25
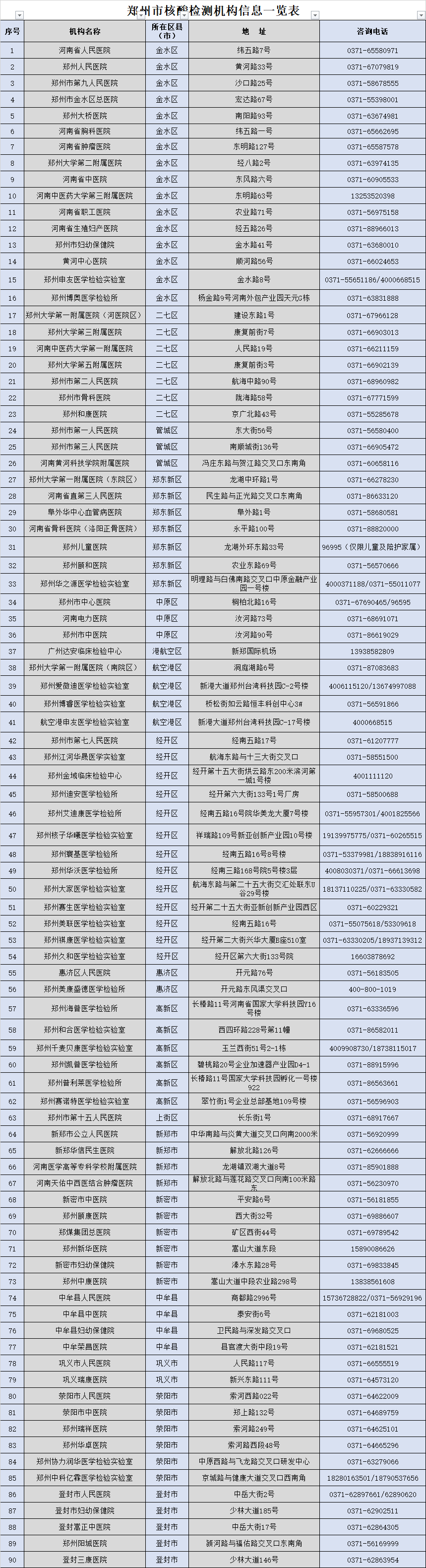
- 本次疫情郑州共开展了十轮全员核酸检测 共2022-01-25
- 噪声污染防治法将于2022年6月5日施行2022-01-25
- 扩散!疫情期间血透预约平台在郑好办App上2022-01-25
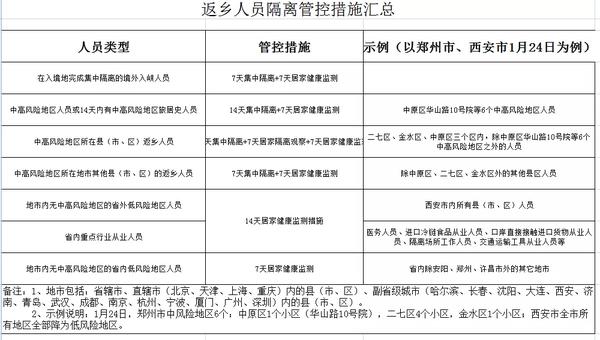
- 速看!三门峡:返乡人员隔离管控措施汇总2022-01-25
- 官方回应:关于禹州市一高一学生反映不能返2022-01-25
- 今年将建30家河南省科普基地 提升广大公众2022-01-25
- 春节前郑州有望全域“低风险” 1月25日起2022-01-25
- 周口郑州新生儿登记排全国前十 王李张等222022-01-25
- 洛阳全面深入推动县管校聘改革 800多所中2022-01-25
- 2022年度一次性工亡补助金标准确定 调整为2022-01-25
- 请乘坐合规车辆!这些网约车非法营运被查处2022-01-25
- 河南:26至28日多地仍有大到暴雪局部暴雪2022-01-25
- 郑州市政府投放储备肉蛋菜 市民购买热情高2022-01-25
- 春节即将来临 郑州市全面禁售禁放烟花爆竹2022-01-25
- 郑州发布2022年32号通告:部分区域疫情风险2022-01-25
- 河南出台“十四五”期间系列养老服务体系“2022-01-25
- 春节前河南将出现一轮长时间大范围的中度至2022-01-25
- 郑州预计除夕前全域降为低风险 春运期间人2022-01-25
- 郑州行程卡何时摘星?调整风险等级及区域解2022-01-25
- 春运期间人员返郑离郑防控政策来了 返郑人2022-01-25
- 郑州发布31号通告:9个城区开展新冠病毒核2022-01-25
- 郑州已解除封控管控隔离群众 可根据病情需2022-01-25